EULER ou ALZHEIMER
J’ai suivi pendant plusieurs années un
charmant patient atteint d’une hypertension artérielle sévère. Je le voyais
régulièrement tous les six mois ,mais un jour sa femme prit un rendez-vous
urgent auprès de ma secrétaire, affirmant que le psychisme de son mari s’était
rapidement détérioré, qu’il ne s’intéressait plus à rien, ne répondait plus aux
questions et qu’il avait probablement une maladie d’Alzheimer évolutive.
Je le vis dès le lendemain et
son comportement semblait effectivement s’être modifié. Après quelques formules
de politesse j’essayai d’explorer ses fonctions
cognitives : « Quelle date sommes-nous ? A quelle adresse
vous trouvez-vous ? Quel est le président de la république ? »
et quelques autres questions élémentaires. Je ne pus obtenir aucune réponse
et sa femme paraissait presque satisfaite que mon examen corrobore ses dires.
L’absence totale de réponse
m’intrigua .Son examen clinique était normal .Il avait une formation
d’ingénieur , était un ancien
polytechnicien et je me hasardai à
tester ses connaissances mathématiques :
- Quelle est la formule
qui correspond à la somme des n premiers nombres ?
- n x (n+1) /2 , soit 5050 pour les 100 premiers nombres , me
répondit il presque confidentiellement.
-Quelle est l'identité d' Euler?-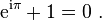
enfin docteur c’est élémentaire !
Je tentai une troisième question :
- Quelle est la probabilité
de gagner au loto ?
-Le Loto me répondit-il
consiste à tirer 6 numéros parmi 49 .La probabilité de gagner et donc de 6 × 5
× 4 × 3 × 2 × 1 / 49 × 48 × 47 × 46 × 45 × 44, soit environ 7 chances sur
100 millions, c’est pour cette raison que les gagnants sont si rares.
- Prodigieux ! Mais, mon cher Monsieur, pourquoi ne répondez
vous pas aux questions plus simples et
ne parlez vous plus à votre femme ?
- Parce qu' elle
m’ennuie avec toutes ses questions stupides et que je ne supporte plus qu’on me
prenne pour un imbécile .
